钽薄壁管焊接成形前期开口间隙场计算的有限元模型
张 景1 , 周方明1 ,2 , 谭一炯1 , 钱乙余2
(1. 江苏科技大学材料科学与工程学院, 江苏镇江212003 ;
2. 哈尔滨工业大学现代焊接生产技术国家重点实验室,黑龙江哈尔滨150001)
摘 要: 为了控制钽薄壁管焊接成形的质量,进行钽薄壁管开口间隙场计算模型的研究。借助有限元方法、薄壳理论以及平板弯曲理论,得到整体单元的刚度矩阵,建立了钽薄壁管开口间隙场计算的有限元模型。该模型精确描述了钽薄壁管焊前成形开口间隙的形状,利用该模型可以系统地研究钽薄壁管焊前成形的过程,为正确地选择成形工艺参数提供了理论依据。试验表明,理论计算与实测结果吻合得较好。
关键词:开口间隙; 有限元; 焊接; 钽薄壁管
0 引 言
钽是一种塑性较好,具有极好的耐酸、碱和液态金属等优越性能的难熔稀有金属[1 ,2 ] 。鉴于钽的特殊性质,钽薄壁管可用于火电、核电、航天等领域。目前关于直缝焊管的成形只局限于接触应力分析[3 ,4 ] 和辊轧成形机理[5 ,6 ] 的研究,关于钽焊接的数学模型,仅有法国的K. Girard 等建立了焊接时气孔形成和消失的模型[7 ] 。钽直缝薄壁管焊接成形前期开口间隙场的计算,在国内外都没有进行深入的研究。为了进一步提高钽薄壁管焊接成形的质量,保证成形的稳定性,充分利用计算机和数值模拟技术,对钽薄壁管焊接前成形开口间隙进行深入系统的理论研究。文中采用有限元法,充分考虑了成形时的条件和材料的性质,建立了钽薄壁管的有限元模型,实现了开口间隙场的计算,为钽管的成形控制提供了有效理论,进而为其生产线的质量控制奠定了基础。
1 直缝薄壁管焊接成形基本原理
直缝薄壁管焊接成形过程是:首先,一定长度的板带在成形机组上经由不同形状的轧辊轧压成形为开口管,形状如图1 所示;然后,开口管在轧辊挤压下,采用TIG电弧加热熔化并在轧辊挤压下冷却成形而获得焊接管。开口管焊接成形如图2 所示。钽薄壁管的成形与材料的物理性能密切相关,在成形时易出现回弹、纵向瓢曲[6 ] 。实践证明,焊管成形时合适的间隙对焊接有利。若间隙太小,容易形成虚焊;太大时发生烧穿,使焊缝组织变化,影响焊接强度及使用寿命;若无间隙会形成错边。为了节约材料和保证焊接质量,必须在焊接前考虑开口间隙[8 ] 。

2 间隙场计算的有限元模型
2.1 前提条件
在钽管的焊接成形中,位移是一个影响焊接质量的重要参数。实际生产中,焊接前要进行钽管的压合,针对实际的焊接成形过程,文中仅取出其中一部分进行建模与分析。
为简化计算,在数学模型建立前假定: ①壳体的挠度与厚度相比很小,在几何方程中的二阶项与高阶项均可略去。②中面的法线在壳体变形后依然与中面正交;壳体的法向线元在壳体变形中保持直线且不发生伸长或缩短。③垂直中面的应力分量与其它的应力分量相比小得可以忽略不计。
对于常用的钽薄壁管,其厚径比满足t/ Rminn 1 ,故可将其看成是壳体而将问题进行简化[9 ] 。考虑到模型的对称性,仅取一半进行分析,将之划分为有限个单元,文中采用4 结点4 边形单元(见图3) 。壳体可以看成是平面应力单元和平板弯曲单元的组合,因此整体单元刚度矩阵由这2 种单元的刚度矩阵组合而成[10 ] 。

2.2 平面应力状态分析
文中采用最常用的三角形单元进行分析。3 个结点按逆时针的顺序编码为i , j , m。在弹性力学平面问题中,每个结点有2 个位移分量,即:
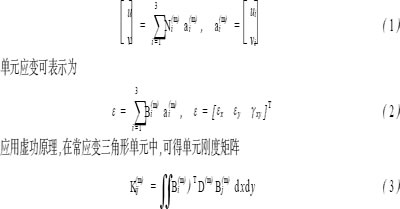
式中:B为应变矩阵, D为系数行列式, N为单元的形函数, K为单元刚度矩阵,ε为单元应变, t是厚度,上标m 表示属于薄膜应力状态。
2.3 对于平板弯曲状态分析
基于板的厚度比其他两个方向尺寸小的多, 以及挠度比厚度小的多的假设, 忽略厚度方向的正应力;薄板中面内的各点没有平行于中面的位移;薄板中面的法线在变形后仍保持为法线。利用假设,平板弯曲问题简化为二维问题,将挠度ω,法线绕x 轴的转动θx 和绕y 轴的转动θy 表示为

式中:ω为单元的挠度;θ为法向的转动;κ为广义应变; K为单元刚度矩阵;上标b 表示属于平板弯曲状态。
2.4 整体刚度单元矩阵
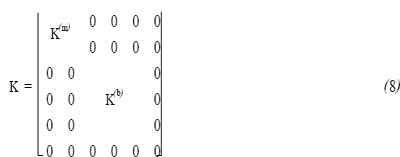
综合上面的两种状态得到平面壳体的刚度单元矩阵为:
2.5 边界条件与有限元网格划分
有限元计算网格的划分对有限元分析的计算精度和计算效率有重要影响。文中考虑到对于常用的钽薄壁管,其厚径比满足t/ Rminn 1 ,故可将其看成是壳体而将问题进行简化[9 ] 。考虑到模型的平面对称性,仅取一半进行分析,将之划分为有限个单元,采用4 结点4 边形单元(见图3) 。将边界条件引入,这里主要考虑了支承条件,可以表示为:
u( x = 0 , y =0) = 0 θxi ( x = 0 , y =0) = 0 (9)
将对称条件引入,在x = 0 , z = 0 ,加入对称约束条件。
2.6 施加载荷的处理
钽管实际辊轧成形是一个动态过程,钽管主要承受辊轮的挤压力,文中将挤压力考虑成为分布不均匀的环向力(图3) ,可以表示为
F( z0 ) = Px (10)
其中: z0 为轧辊的位置, Px 为施加的压力。
3 数值计算结果的验证
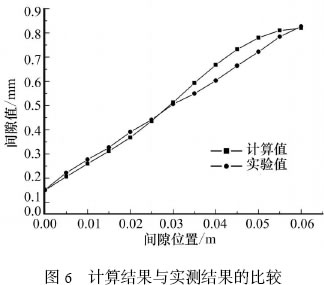
钽薄壁管焊接是一个动态过程,并且在同一个位置可能存在微小的变化,因此直接测量开口间隙比较困难。文中采用现场拍照,并根据比例条件进行校核,取其平均值的方法验证数据的准确性。计算过程中充分考虑实际条件,采用合适的简化与假设。利用大型有限元软件ANSYS 针对具体条件进行计算并与实验值进行比较。试件取为壁厚0.5 mm 的钽薄壁直缝钽管。图6 是计算结果与实测结果的比较,表明两者吻合得较好。
4 结 论
1) 文中所建立的钽薄壁管焊接前期开口间隙场的有限元模型,可以精确描述薄壁钽管焊接成形前期开口间隙的形状,充分考虑辊轧力、对称、约束对间隙的影响,从而实现了对薄壁钽管焊接成形前期开口间隙的数值分析。
2) 计算结果与实测结果比较表明,二者吻合得较好。因此,所建的数值模型有较高的精度。
3) 薄壁钽管焊接成形前期开口间隙场的有限元模型的建立,为钽薄壁管生产线过程中焊接质量的控制奠定了基础。
|
