|
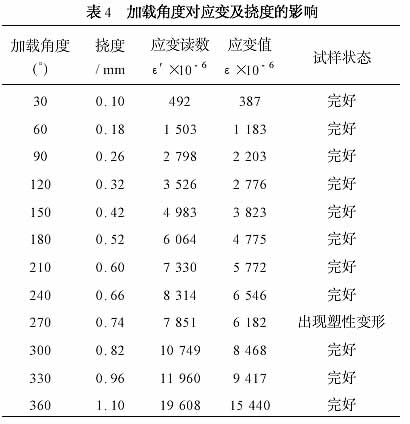
“三点弯曲”试验加载角度与应变的关系见表4和图4,卸载过程应变读数见表5 。由图4 可见,随着加载角度的增大,试样的应变值逐渐增大,经过近似直线的弹性范围后,在加载角度为240°~270°时,应变发生突变,达到塑变区;继续加载到加载角度为360°时应变值为15 440 ×10 - 6 。
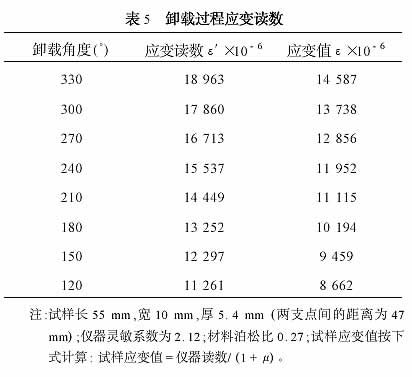
卸载过程中,应变直线下降;卸载完成后,残余变形恒定, 应变值为8 662 ×10 - 6 , 为塑性变形。所以HQ130 钢的弹性变形为6 778 ×10 - 6 。合金钢的弹性模量E 为186~206 GPa[5] ,由σs = E(εe-εT-εs) 可得,σs为1 260.7~1 396.3 MPa。式中εe 为可见变形率,εT 为自由热变形率,εe-εT - εs为屈服变形率。常温下HQ130 钢的σs为1 313 MPa ,处于此范围之内,表明所得到的试验数据可靠。根据公式E =σs/(εe-εT-εs),将HQ130 钢的σs ( 1 313 MPa) 和弹性变形ε(6 778×10-6) 代入可得,常温下HQ130 钢的弹性模量E为1.94×10(5) MPa 。
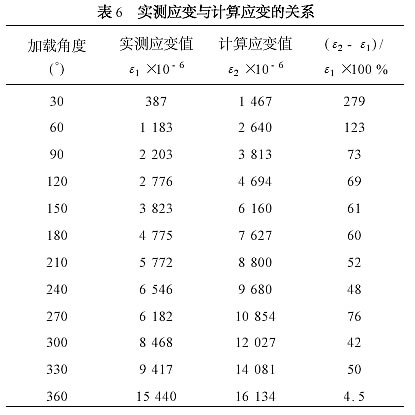
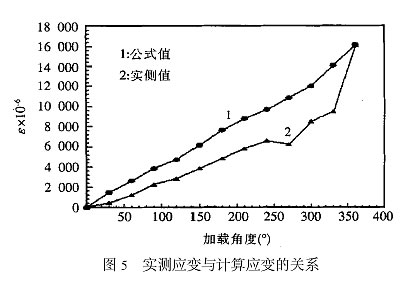
实测应变与计算应变的关系见表6和图5,应变的公式计算值大于实测值279%~4.5%。差值百分比在初始加载时和塑变发生时较大(已失去实际意义) ,塑变发生后随着应变的增大,差值百分比变小,当加载角度达到360°时,差值百分比只有4.5 %。

发生上述现象可能是由下列原因造成的: ①试样在屈服点以前就发生了塑性变形,而所用公式为完全弹性公式,所以公式值与实测值有偏差; ②用千分尺测挠度,易产生误差; ③垫块和螺杆端部磨制得比较薄,加力之初,垫块和螺杆易于变形,所以偏差较大;到加大角度后,垫块和螺杆变形变得困难,偏差较小。
尽管应变的公式计算值和实测值之间存在着一定的偏差,但二者的总体趋势是一致的,在要求不太严格或只要求获得应变变化规律的情况下,仍可用公式法粗略估算。
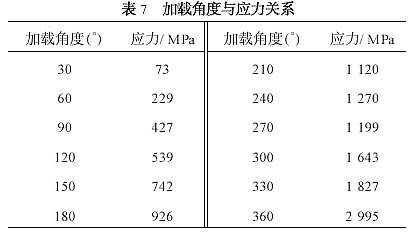
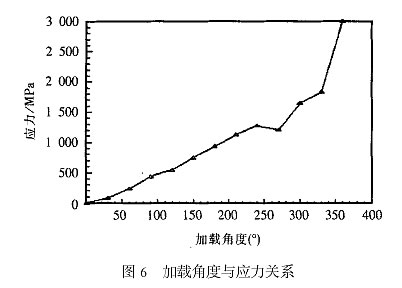
在弹塑性范围内,应力σ= E(εe-εT-εs)。将所测应变及HQ130 钢的E 值代入可得各加载角度对应的应力值,见表7 。由图6 和表7 可见,随着外加载荷的增加,试样内产生的应力逐步增大。当加载角度为240°~270°时,应力有下降的趋势,这是由于应力值是根据弹性关系得出的,而此时试样已发生了塑性变形,故应力值比实际值要偏小一些;随后应力值又逐步增大,直至超过HQ130 钢的屈服极限。所测应力值大于HQ130 钢的拉伸强度σb (1 370 MPa) 而试样却未裂,是由于此时计算应力用的是弹性模量E ,实际上应该用塑性模量E′,一般情况下E′n E ,故计算应力远远大于实际应力,塑变以后偏差可能更大。
在金相显微镜下观察经“三点弯曲”后的试样发现,焊缝中先共析铁素体有规律的发生弯曲,弯曲方向与试样弯曲方向一致,而针状铁素体与珠光体无明显变形。熔合区附近的原奥氏体晶界沿变形方向有所拉长,由原来的近似六边形变化为近似长方形;垂直于熔合区成长的组织发生一定角度的偏移,偏移方向与试样的变形方向相同。随加载力的增大,这些组织的变形增大,方向性增强。熔合区附近的低碳马氏体组织较粗大,裂纹沿条状组织扩展比横穿条状组织容易,故裂纹在此处扩展所需的能量小,容易在此处产生。“三点弯曲”试验表明,外加载荷促进了熔合区附近裂纹的产生和扩展。
焊接熔合区存在着的相界、杂质和微观缺陷是潜在的裂纹源,在应力的作用下形成应力集中的三向应力区,当应力进一步增大时,促使缺陷扩展而形成裂纹。微裂纹尖端又作为应力集中部位使新的位错在其周围聚集,随变形量的增大又产生新的裂纹扩展。高强钢焊接裂纹从孕育、萌生、扩展以至开裂,由许多单个间歇式的微裂纹汇合而成,裂纹扩展是不连续的。
3 结 论
(1)“三点弯曲”试验结果表明,外加载荷增大,焊接试样的应力应变值逐渐增大,经过近似直线的弹性范围后,达到塑变区后应变发生突变。
(2) 所测应力值大于HQ130 钢的拉伸强度σb(1 370 MPa) 时试样却未裂,是由于计算应力用的是弹性模量E , 实际上应该用塑性模量E′, 一般情况下E′n E ,故计算应力远远大于实际应力。
(3) 尽管应变的公式计算值和实测值之间存在着一定的偏差,但二者的总体趋势是一致的,在要求不太严格或只要求获得应变变化规律的情况下,仍可用公式法估算。
|
