|
2 机构动刚度的计算
假设在D点有作用外力Fx和Fy,则机构的动力学方程为:
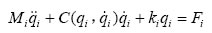
式中Fi为末端点外力矢量(Fx和Fy)。
由于IC芯片粘片机的运动速度快,频率较高(超过2万次/h),则得到新的动力学方程为:

根据文献[8],机构的动刚度可以定义为:
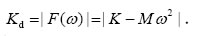
假设焊头座末端D点以角频率ω振动,且振幅的模为1,则由式(1)可以得出:
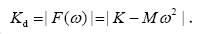
从上式可知,振动频率逐步增大时,动刚度将慢慢减小;当频率达到某个值后,动刚度将降为零,此时即发生了共振,有

因此,研究机构的动刚度可转换为研究其共振频率。如图3所示,在动点D的平衡位置建立坐标系(坐标原点为平衡点),则系统的振动微分方程为:
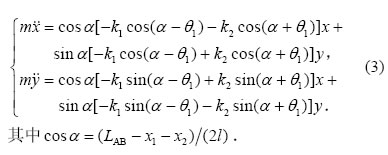
当粘片机的焊头机构在某一固定位置时,cosα和sinα为定值,则(4)式是一个二阶常系数微分方程,设其特解为:
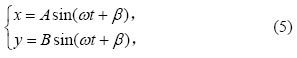
其中A和B是振幅,ω为固有圆频率,β是初相位。将(5)式代入(4)式中,解得

将(6)式代入(2)式即可求出系统的动刚度,它仅与k1,k2和 α 有关,即取决于系统所处的位置和杆件的弹性,而与起始条件和外加激振力无关。 |
